
| Home | People | Research | Publications | Demos |
| News | Jobs |
Prospective
Students |
About | Internal |

| Measuring Image Manifold Distances | |
|
|
|
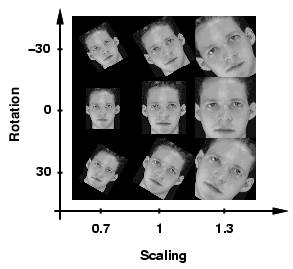
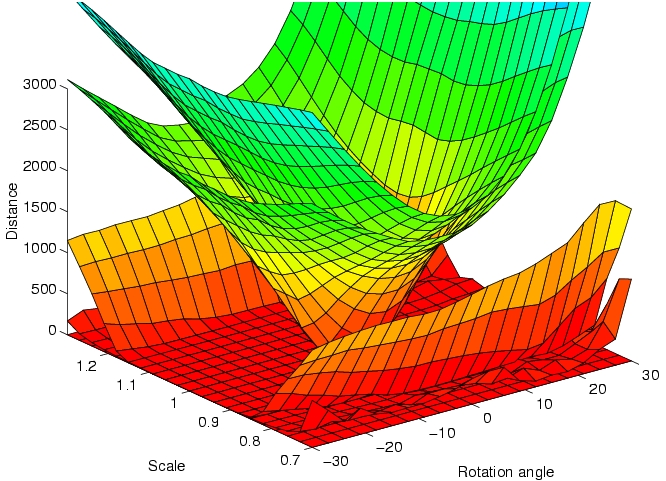
The ability to measure distances between images (and video) is a fundamental pre-requisite from most problems involving their classification and retrieval. For example, given a set of distances associated with a set of images, it is usually possible to build a classifier by simple application of off-the-shelf classification architectures. However, measuring image distances in a sensible way is a complex task. The reason is that not all forms of image variability are equal: while all variation of image intensity due to a change of subject should result in an increased distance, the latter should be invariant to all changes of intensity that can occur for the same subject. Consider, for example the problem of comparing two face images. Assuming the representation of each image as a point in Euclidean space, the distance between two images of the same person (e.g. a frontal and a profile view) can be much larger than that between images of two people (e.g. when both are frontal views). Mathematically, when images are subject to spatial transformations (rotations, scaling, changes of subject pose, etc.) or variable lighting, they span manifolds in the high-dimensional Euclidean space of pixel intensities. Hence, the "correct" measure of distance is one that measures the distance between the manifolds resulting from all possible transformations of the images, rather than the Euclidean distance between the images themselves. This idea has been formalized in the machine learning literature through the introduction of the so-called "tangent distance" (which is the distance between the manifold tangents at the location of the images). The tangent distance has, however, been shown to exhibit some important limitations, namely the inability to deal with large transformations and a pronounced lack of robustness to the presence of outliers (e.g. subject with glasses on image A vs. subject without glasses on image B). This project studies various extensions to the tangent distance. In particular, we embed it into a multi-resolution framework that makes it significantly less prone to local minima. The new metric - multi-resolution tangent distance - can be easily combined with robust estimation procedures, and exhibits significantly higher invariance to image transformations than the tangent and Euclidean distances. This translates into significant improvements in classification accuracy. |
|
| Selected Publications: |
|
| Demos/ Results: |
|
| Contact: | Nuno Vasconcelos |
![]()
©
SVCL