![]()
| Multiclass Boosting: MCBoost | ||||
| In this project the problem of multi-class boosting is considered. A new framework, based on multi-dimensional codewords and predictors is introduced. The optimal set of codewords is derived, and a margin enforcing loss proposed. The resulting risk is minimized by gradient descent on a multidimensional functional space. Two algorithms are proposed: 1) CD-MCBoost, based on coordinate descent, updates one predictor component at a time, 2) GD-MCBoost, based on gradient descent, updates all components jointly. The algorithms differ in the weak learners that they support but are both shown to be Bayes consistent and margin enforcing. They also reduce to AdaBoost when there are only two classes. Experiments show that both methods outperform previous multiclass boosting approaches in a number of datasets. | ||||
| Key Idea: | ||||
In binary classification we learn a function f(x) which is positive for one class and negative for the other class. This means that f(x) is a transformation that pushes example of the first class toward direction of vector +1 and examples of the other class toward direction of vector -1. |
||||
 |
||||
| Using this observation, for multiclass boosting, e.g. 3 classes, we need to push examples in three different directions. | ||||
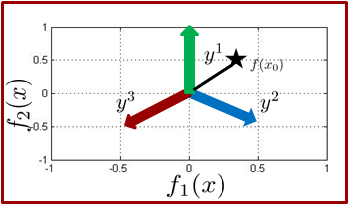 |
||||
| In our paper we showed that for a M-class classification problem, the optimal set of directions will form a simplex in M-1 dimensions. Below you can see examples of those directions for M = 2, 3, 4. | ||||
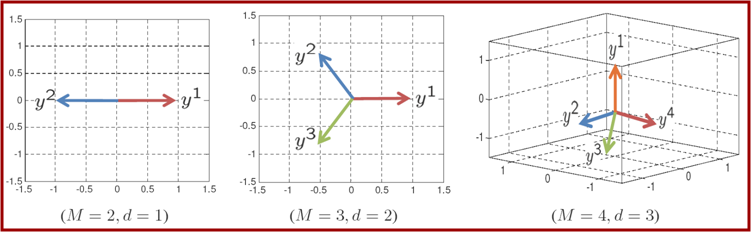 | ||||
| Using this idea we have developed MCBoost method. The following video shows evaluation of MCBoost predictor with the number of iterations for a synthetic toy dataset. In the begining all example are mapped to origin but as the algorithm proceed, MCBoost pushes examples of different classes toward pre-specified directions. Please see the related publication for more details and mathematical formalism. | ||||
| Download | ||||
| Related Publications: | ||||
|
![]()
Copyright
@ 2009 www.svcl.ucsd.edu
