|
The machine learning problem of classifier design is studied from the perspective
of probability elicitation, in statistics. This shows that the standard approach of
proceeding from the specification of a loss, to the minimization of conditional
risk is overly restrictive. It is shown that a better alternative is to start from the
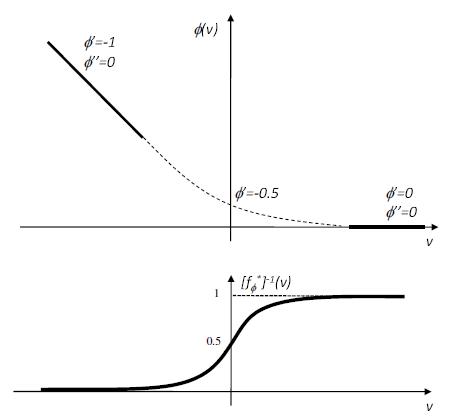
specification of a functional form for the minimum conditional risk, and derive
the loss function. This has various consequences of practical interest, such as
showing that 1) the widely adopted practice of relying on convex loss functions is
unnecessary, and 2) many new losses can be derived for classification problems.
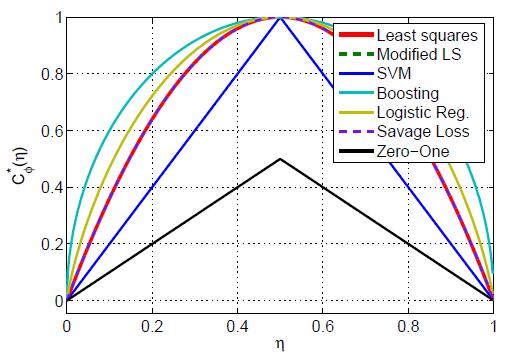
These points are illustrated by the derivation of a number of novel Bayes consistent loss functions, some of which are not convex
but do not compromise the computational tractability of classifier design. A number of algorithms custom tailored for specific classification problems
are derived based on novel loss functions. These include classification algorithms for cost sensitive learning, robust outlier resistant classification and variable margin classification.
| Algorithms: |
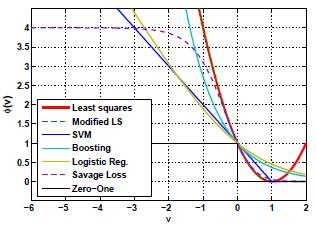
SavageBoost
A new boosting algorithm,
SavageBoost, is derived for the minimization of the novel Savage loss. This boosting algorithm which is based on the bounded and nonconvex Savage loss function
is less sensitive to outliers than conventional methods, such as
Ada, Real, or LogitBoost, and converges in fewer iterations.
| |
|
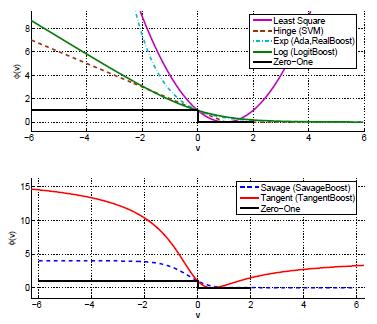
TangentBoost
A new boosting algorithm,
TangentBoost, is derived for the minimization of the novel Tangent loss. The bounded and nonconvex Tangent loss function penalizes both large positive and negative
margins which results in a much more robust classifier suitable for computer vision datasets with noisy data.
| |
|
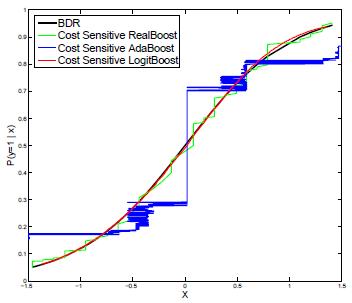
Cost Sensitive Boosting
The new cost sensitive AdaBoost, RealBoost and LogitBoost algorithms are derived based on the novel cost sensitive Bayes consistent exponential and logistic losses.
| |
|
Cost Sensitive SVM
The new cost sensitive SVM algorithm is derived based on the novel cost sensitive Bayes consistent hinge loss.
| |
|
Variable Margin Canonical GradientBoost
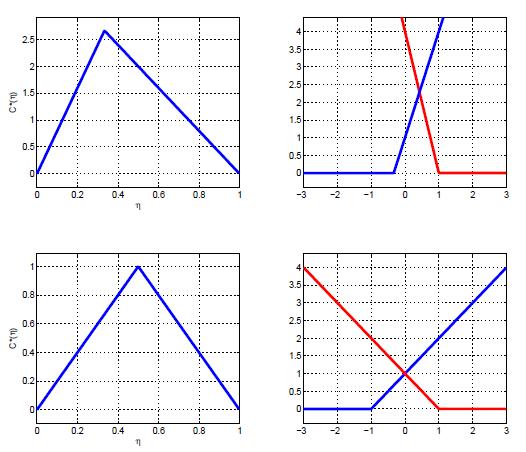
A detailed analytical study is presented on how properties of the classification risk, such as
its optimal link and minimum risk functions, are related to the shape of the loss, and its margin enforcing properties.
Novel families of Bayes consistent loss functions, of variable margin, are derived. These families are then used to design
boosting style algorithms with explicit control of the classification margin.
| |
|
|
| Publications: |
Cost-Sensitive Boosting.
Hamed Masnadi-Shirazi and Nuno Vasconcelos
IEEE Trans. on Pattern Analysis and Machine Intelligence,
vol. 32(2), 294, March 2010 .
IEEE
[ps]
[pdf]
Variable margin losses for classifier design.
Hamed Masnadi-Shirazi and Nuno Vasconcelos.
Neural Information Processing Systems (NIPS), Vancouver, Canada, Dec 2010.
(acceptance rate 25%)
[pdf]
Risk minimization, probability elicitation, and cost-sensitive SVMs
Hamed Masnadi-Shirazi and Nuno Vasconcelos.
International Conference on Machine Learning (ICML), 2010.
(acceptance rate 20%)
[pdf]
On the Design of Robust Classifiers for Computer Vision.
Hamed Masnadi-Shirazi, Nuno Vasconcelos and Vijay Mahadevan.
IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2010.
Oral presentation (acceptance rate 5%)
CVPR Oral presentation video
[pdf]
On the Design of Loss Functions for Classification: theory, robustness to outliers, and SavageBoost.
Hamed Masnadi-Shirazi and Nuno Vasconcelos
Proceedings of Neural Information Processing Systems (NIPS),
Vancouver, Canada, Dec 2008.
[pdf]
Asymmetric Boosting
Hamed Masnadi-Shirazi and Nuno Vasconcelos
Proceedings of International Conference on Machine Learning (ICML),
Corvallis, OR, May 2007.
[pdf]
| Contact: |
Nuno Vasconcelos, Hamed Masnadi-Shirazi
|
| |


![]()